Authors: Zongyi Li, Daniel Zhengyu Huang, Burigede Liu, Anima Anandkumar

Published on: May 03, 2024

Impact Score: 7.8

Arxiv code: Arxiv:2207.05209

Summary

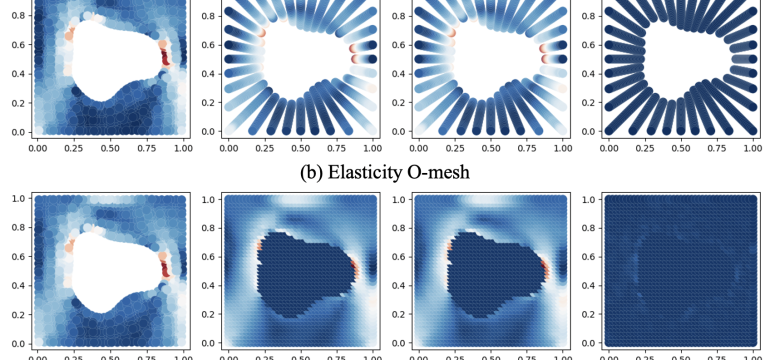
• What is new: A new framework, geo-FNO, that can solve PDEs on arbitrary geometries, improving both the speed and accuracy of solutions compared to existing methods.
• Why this is important: Existing deep learning models like the Fourier neural operator (FNO) are limited to rectangular domains with uniform grids, restricting their application to complex geometries.
• What the research proposes: Geo-FNO expands the application of FNO to irregular geometries by deforming the input domain into a latent space where the FFT can be applied, making it versatile and efficient.
• Results: Geo-FNO achieved a speed 100,000 times faster than standard numerical solvers and was twice as accurate compared to existing ML-based PDE solvers like the standard FNO.

Technical Details

Technological frameworks used: Geo-FNO

Models used: Fourier Neural Operator (FNO) with Fast Fourier Transform (FFT)

Data used: Point clouds, meshes, and design parameters

Potential Impact

Engineering design and simulation software, aerospace, civil engineering, and any industry relying on PDE modeling for fluid dynamics or material science.

Want to implement this idea in a business?

We have generated a startup concept here: GeoSimTech.