Authors: Zhanhong Ye, Xiang Huang, Leheng Chen, Hongsheng Liu, Zidong Wang, Bin Dong

Published on: February 20, 2024

Impact Score: 7.8

Arxiv code: Arxiv:2402.12652

Summary

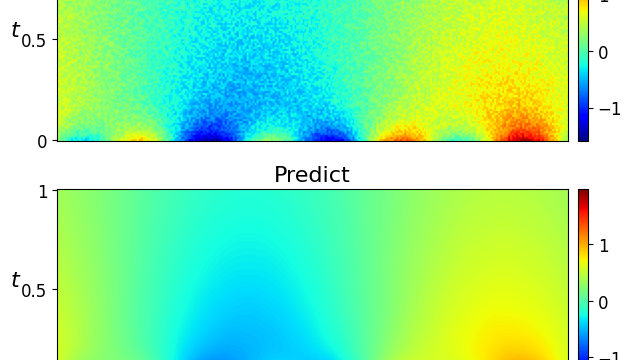
• What is new: Introduction of PDEformer, a neural solver capable of dealing with various types of PDEs using a computational graph, a novel approach compared to existing methods.
• Why this is important: Existing PDE solvers struggle with versatility and integration of symbolic and numerical information.
• What the research proposes: PDEformer employs a computational graph, a graph Transformer, and implicit neural representation to provide mesh-free predicted solutions.
• Results: Achieves zero-shot accuracies that surpass those of expert models trained for specific tasks; shows promise in solving inverse problems like PDE coefficient recovery.

Technical Details

Technological frameworks used: Graph Transformer, Implicit Neural Representation (INR)

Models used: PDEformer

Data used: Diverse benchmark datasets for training and zero-shot accuracy testing

Potential Impact

Computational engineering firms, simulation software companies, and industries requiring PDE solutions (e.g., aerospace, climate modeling, and finance)

Want to implement this idea in a business?

We have generated a startup concept here: InfiniSolve.